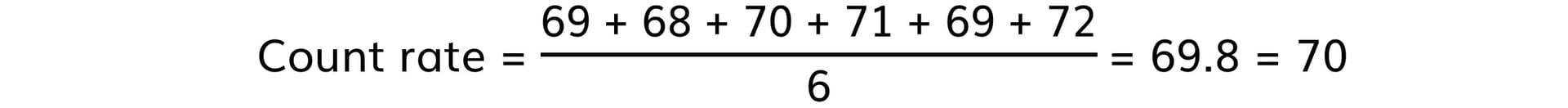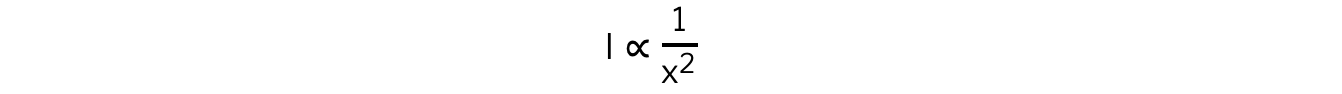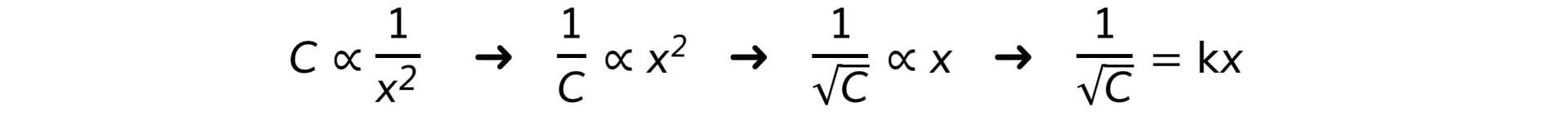A student measures the background radiation count in a laboratory and obtains the following readings:

The student is trying to verify the inverse square law of gamma radiation on a sample of Radium-226. He collects the following data:
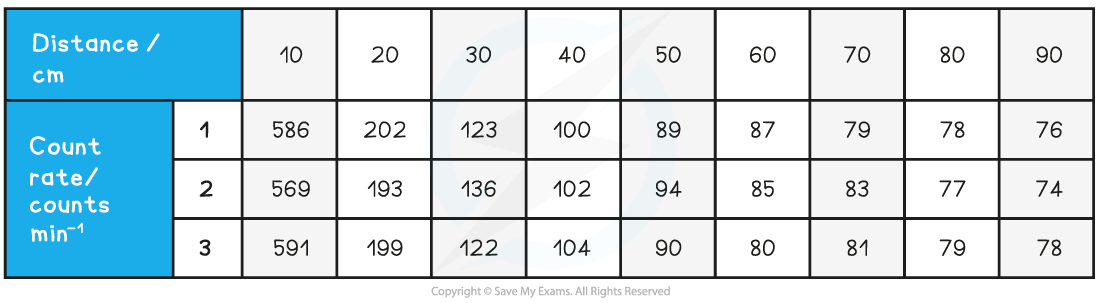
Use this data to determine if the student’s data follows an inverse square law.
Answer:
Step 1: Determine a mean value of background radiation
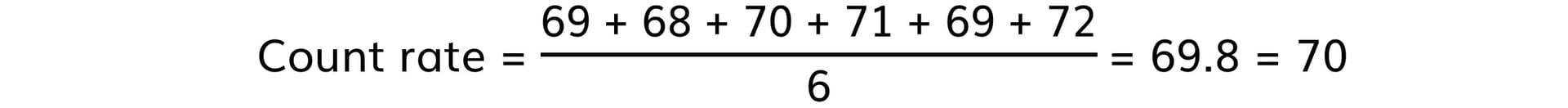
- The background radiation must be subtracted from each count rate reading to determine the corrected count rate, C
Step 2: Compare the inverse square law to the equation of a straight line
- According to the inverse square law, the intensity, I, of the γ radiation from a point source depends on the distance, x, from the source
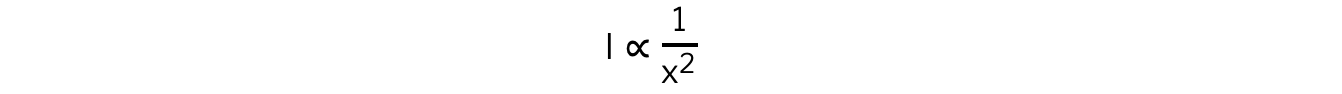
- Intensity is proportional to the corrected count rate, C, so
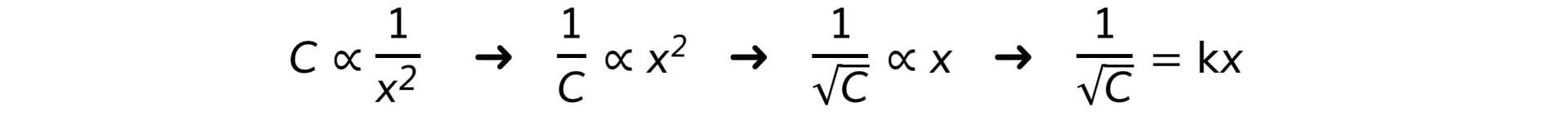
- The graph provided is of the form 1/C–1/2 against x
- Comparing this to the equation of a straight line, y = mx
- y = 1/C–1/2 (counts min–1/2)
- x = x (m)
- Gradient = constant, k
- If it is a straight line graph through the origin, this shows they are directly proportional, and the inverse square relationship is confirmed
Step 3: Calculate C (corrected average count rate) and C–1/2
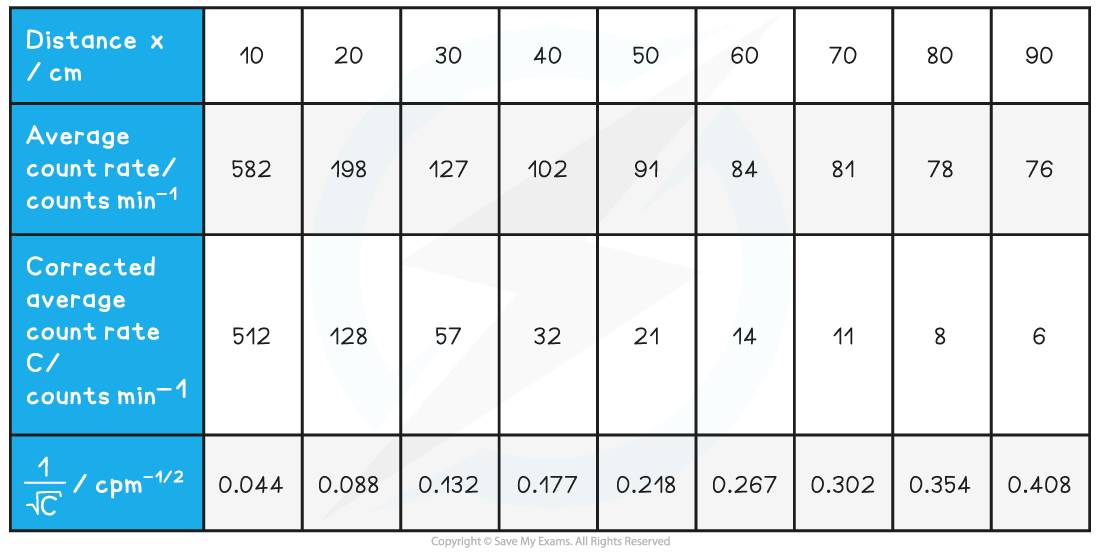
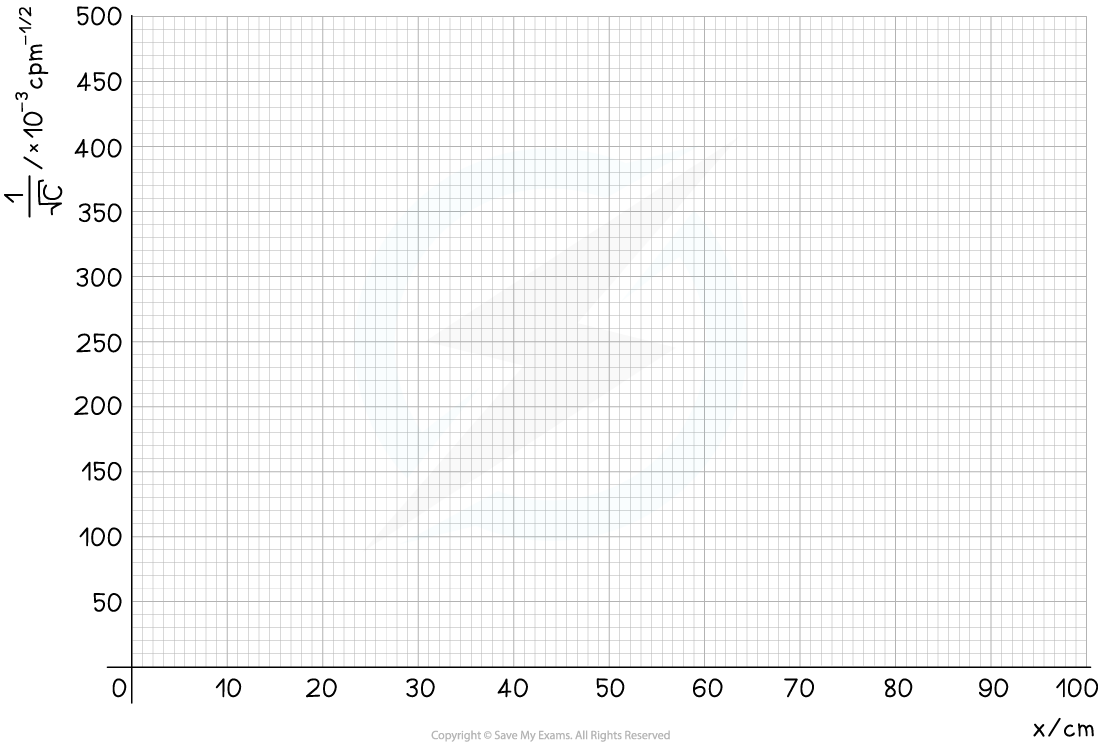
Step 4: Plot a graph of C–1/2 against x and draw a line of best fit

- The graph shows C–1/2 is directly proportional to x, therefore, the data follows an inverse square law