Symmetry of Functions (DP IB Maths: AA HL)

Revision Note

Download PDF

Test yourself Flashcards

Author

Dan

Expertise

Maths

Did this video help you?

Odd & Even Functions

What are odd functions?

A function $f (x)$ is called odd if

$f (- x) = - f (x)$ for all values of $x$

Examples of odd functions include:

Power functions with odd powers: $x^{2 n + 1}$ where $n \in ℤ$

For example: ${(- x)}^{3} = - x^{3}$

Some trig functions: $\sin x$ , $cosec x$ , $\tan x$ , $\cot x$

For example: $\sin (- x) = - \sin x$

Linear combinations of odd functions

For example: $f (x) = 3 x^{5} - 4 \sin x + \frac{6}{x}$

What are even functions?

A function $f (x)$ is called even if

$f (- x) = f (x)$ for all values of $x$

Examples of even functions include:

Power functions with even powers: $x^{2 n}$ where $n \in ℤ$

For example: ${(- x)}^{4} = x^{4}$

Some trig functions: $\cos x$ , $\sec x$

For example: $\cos (- x) = \cos x$

Modulus function: $| x |$
Linear combinations of even functions

For example: $f (x) = 7 x^{6} + 3 |x| - 8 \cos x$

What are the symmetries of graphs of odd & even functions?

The graph of an odd function has rotational symmetry

The graph is unchanged by a 180° rotation about the origin

The graph of an even function has reflective symmetry

The graph is unchanged by a reflection in the y-axis

Exam Tip

Turn your GDC upside down for a quick visual check for an odd function!
- Ignoring axes, etc, if the graph looks exactly the same both ways, it's odd

Worked example

The graph

y = f (x)

is shown below. State, with a reason, whether the function

f

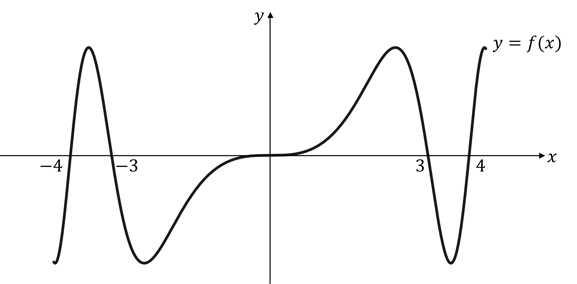
is odd, even or neither. 2-3-3-ib-aa--ai-we-image-a

2-3-3-ib-aa-hl-odd-even-functions-a-we-solution

Use algebra to show that

g (x) = x^{3} \sin (x) + 5 \cos (x^{5})

is an even function.

2-3-3-ib-aa-hl-odd-even-functions-b-we-solution

Did this video help you?

Periodic Functions

What are periodic functions?

A function $f (x)$ is called periodic, with period k, if
- $f (x + k) = f (x)$ for all values of $x$
Examples of periodic functions include:
- sin x & cos x: The period is 2π or 360°
- tan x: The period is π or 180°
- Linear combinations of periodic functions with the same period
  - For example: $f (x) = 2 \sin (3 x) - 5 \cos (3 x + 2)$

What are the symmetries of graphs of periodic functions?

The graph of a periodic function has translational symmetry

The graph is unchanged by translations that are integer multiples of $(\begin{matrix} k \\ 0 \end{matrix})$
The means that the graph appears to repeat the same section (cycle) infinitely

2-3-3-ib-aa-hl-periodic-functions

Exam Tip

There may be several intersections between the graph of a periodic function and another function
- i.e. Equations may have several solutions so only answers within a certain range of $x$ -values may be required
  - e.g. Solve $\tan x = \sqrt{3}$ for $0 ° \leq x \leq 360 °$
  - $x = 60 °, 240 °$
- Alternatively you may have to write all solutions in a general form
  - e.g. $x = 60 (3 k + 1) °, k = 0, \pm 1, \pm 2, . . .$

Worked example

The graph $y = f (x)$ is shown below. Given that $f$ is periodic, write down the period.

2-3-3-ib-aa--ai-we-image-c

2-3-3-ib-aa-hl-periodic-functions-we-solution

Did this video help you?

Self-Inverse Functions

What are self-inverse functions?

A function $f (x)$ is called self-inverse if

$(f \circ f) (x) = x$ for all values of $x$
$f^{- 1} (x) = f (x)$

Examples of self-inverse functions include:

Identity function: $f (x) = x$
Reciprocal function: $f (x) = \frac{1}{x}$
Linear functions with a gradient of -1: $f (x) = - x + c$

What are the symmetries of graphs of self-inverse functions?

The graph of a self-inverse function has reflective symmetry

The graph is unchanged by a reflection in the line y = x

Exam Tip

If your expression for $f^{- 1} (x)$ is not the same as the expression for $f (x)$ you can check their equivalence by plotting both on your GDC
- If equivalent the graphs will sit on top of one another and appear as one
- This will indicate if you have made an error in your algebra, before trying to simplify/rewrite to make the two expressions identical
It is sometimes easier to consider self inverse functions geometrically rather than algebraically

Worked example

Use algebra to show the function defined by $f (x) = \frac{7 x - 5}{x - 7}, x \neq 7$ is self-inverse.

2-3-3-ib-aa-hl-self-inverse-functions-we-solution

Test yourself Flashcards Next topic

Did this page help you?

Symmetry of Functions (DP IB Maths: AA HL)

Revision Note

What are odd functions?

What are even functions?

What are the symmetries of graphs of odd & even functions?

What are periodic functions?

What are the symmetries of graphs of periodic functions?

What are self-inverse functions?

What are the symmetries of graphs of self-inverse functions?

Author: Dan